Quiz
Q1) The net torque will be the same if a force is doubled but moved to a point halfway to the axis of rotation.
A. True
B. False
Answer) A.
Torque is calculated by multiplying Force and distance
Q2) If the resultant of a set of concurrent forces is zero, the sum of the torques
A. is also zero
B. may or may not be zero
C. is not zero
D. depends on the axis of rotation
Answer) A.
The sum of the moments of the forces about the concurrent point is zero, so the sum of the moments about every point is zero. The only condition imposed by equilibrium on a set of concurrent forces is that their sum is zero.
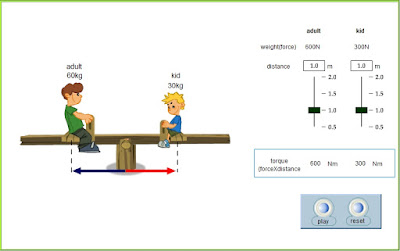
Rotational Equilibrium of seesaw Simulation
When the next simulation is not visible, please refer to the following link.
(https://helpx.adobe.com/flash-player/kb/enabling-flash-player-chrome.html)
Torques
Every time you open a door, turn on a water faucet, or tighten a nut with a wrench, you exert a turning force. These everyday movements are shown in Fig 01. Torque is produced by this turning force and tends to produce rotational acceleration. Torque is different from force. If you want to make an object move, apply a force. Unbalanced forces make things accelerate. To make an object turn or rotate, apply a torque. Torques produce rotation.
Fig 01. A torque produces rotation.
A doorknob is located as far as possible from the door’s hinge line for a good reason.
If you want to open a heavy door, you must certainly apply a force, but that is not enough. Where you apply that force and in what direction you push are also important. If you apply your force nearer to the hinge line than the knob, or at any angle other than 90 to the plane of the door, you must use a greater force than if you apply the force at the knob and perpendicular to the door’s plane.
As an example of what torque means and why it is important, think of the example of a door.
Fig 02. The torque is quite large when the
force is applied far away from the fulcrum.
Fig 03. If the force is applied closer to the
fulcrum, the torque is smaller.
Usually the door knob is placed far away from the fulcrum (where the door is attached to the wall with hinges) as shown in Fig 02. If you pull on the knob to open the door, you have a pretty easy time because the force. You are using causes a lot of torque(twisting) around the fulcrum (hinges) to open the door. Imagine that the door knob is now placed near the center of the door, closer to the hinge, as shown in Fig 03.
If you pull on the door knob with the same force as before, it will be more difficult to open the door. This is because the torque (twisting force) has decreased.
The formula to measure the amount of torque is a short one, but applying it depends on the question being asked.
$\ τ =r\times F$
$\ τ$ = torque (N∙m)
$\ F$ = force (N)
$\ r$ = lever arm distance (m)
At the end of a calculation of torque, it is common to give the torque a positive or negative value, depending on the direction it is turning.
◦ Clockwise (CW) torque = negative
◦ Counterclockwise (CCW) torque = positive
In the Figures shown above, the force was kept constant but the lever arm distance was changed. This is why we did not get as much torque in the second situation.
Fig 04. This scale relies on balanced torques.
Scale balances that work with sliding weights, such as the one shown in Fig 04, are based on balanced torques, not balanced masses. The sliding weights are adjusted until the counterclockwise torque just balances the clockwise torque. Then the arm remains horizontal. We say the scale is in rotational equilibrium.
Balanced Torques
Fig 05. A pair of torques can balance each other.
Torques are intuitively familiar to youngsters playing on a seesaw. Children can balance a seesaw even when their weights are not equal.
Weight alone does not produce a change in rotation—torque does. Children soon learn that the distance they sit from the pivot point is as important as their weight. In Fig 05, the person A sits a shorter distance from the fulcrum (turning axis) while the person B sits farther away. Balance is achieved if the torque that tends to produce clockwise rotation by the person A equals the torque that tends to produce counterclockwise rotation by the person B. When balanced torques act on an object, there is no change in rotation.